遥か過去から数学者たちは「方程式を解く」ことに全力を注いできました。
2次方程式は紀元前1800年頃に解の仕組みが発見され、ルネサンス期には3次や4次の解法も確立しました。
しかし、5次以上の多項式だけは、どうしてもルートを使って表せないことが、19世紀に判明します。
すなわち2次、3次、4次方程式と同じように「5次は解けない」ということが、長らく数学界の定説だったのです。
ところがオーストラリアのニューサウスウェールズ大学(UNSW)で行われた研究によって、ついにその壁を乗り越える新たなアプローチが発表されました。
新たな方法は数列や図形の概念を使うことで、従来なら「不可能」とされていた2、3、4次方程式と共通した手法で5次方程式以上の解を与えられるというのです。
もしこの新手法が本格的に発展すれば、数学史における「5次方程式の不可能性」の概念が大きく書き換えられるだけでなく、コンピュータを用いた高次方程式の数値解の算出やアルゴリズム開発にも新しい風が吹くかもしれません。
従来の理論では不可能とされた5次方程式が、なぜ今になって“解ける”ようになったのでしょうか?
研究内容の詳細は2025年4月8日に『The American Mathematical Monthly』にて発表されました。
目次
- 5次方程式、なぜ解けなかった?
- 図形と数列で5次方程式の解を作る
- ルートに頼らない代数学――計算機アルゴリズムはどう変わる?
5次方程式、なぜ解けなかった?

2次方程式の解法は紀元前1800年ごろのバビロニア文明でも知られており、現在でも上のようなおなじみの解の公式が導かれています。
3次、4次方程式にも16世紀のカルダノやフェラーリらにより一般解が見つかりましたが、これらはいずれも3乗根や4乗根などの根号を含む極めて複雑な式になります
例えば3次方程式の解はカルダノの公式は上の図に示したように、かなり複雑な形で示されています。
4次方程式にもフェラーリの解法があり、一般的な代数的解は存在しますが、式の複雑さはさらに増します。
2~4次の公式はいずれもルートの存在を前提としています。
なので多くの人々は、何乗しようとそれに合わせてルートのレベルを上げていけば対応できると思いがちです。
しかし不思議なことに5次方程式は4次以下と同じように、ルートを使って表すことができません。
5次方程式の解を導くにはより高度な特殊関数が必要不可欠になるのです。
ルートは2~4次方程式ではXの値を綺麗に解きほぐす包丁となれても、5次ではいくら重ねても解けない最後の1塊のようなものが残ってしまうのです。
多くの人は「えっ、なぜそこから先が急に不可能なの?」と感じるでしょう。
3次や4次の公式があまりに複雑なため、「こんなに複雑なら5次だって理屈の上で頑張ればできるのでは?」という直感が働くかもしれません。
しかしガロア理論では、5次以上の方程式の構造は「根号の繰り返し」でほどけるものとはまったく別次元であると厳密に示されるのです。
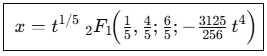
まさにここに不思議な断絶があり、数学史の大きな壁としてあらゆる研究者を阻んできました。
ところが今回研究者たちは、この「5次以上は不可能」という伝統的定説に対し、根号ではなく数列や図形的な概念を使うことで4次と5次を飛び越えられる「一般的な解」を形式的に導こうとする新アプローチに挑みました。
図形と数列で5次方程式の解を作る

新しいアプローチのキーポイントは、「組み合わせの数を数える特殊な数列」を活用することです。
まず、たとえば「カタラン数」と呼ばれる有名な数列があります。
これは大きな多角形を何本かの線で三角形に切り分けるときに、その線が交わらないようにする方法がいくつあるかを数え上げるものです。
実はこのカタラン数には2次方程式(高校数学で習う)との間に深いつながりがあることがわかっています。
論文著者であるワイルドバーガー教授によれば、「カタラン数は2次方程式と密接に関係しているので、5次以上を扱うにはもっと進化した“カタラン数の仲間”を探す必要がある」というわけです。
教授らはさらに発想を広げ、三角形だけでなく四角形や五角形などを含む形で多角形を分割する場合の数を表す「ハイパーカタラン数」を定義しました。
これは、三角形のときのカタラン数をより大きく一般化したものと考えていただくとイメージしやすいです。
そして、このハイパーカタラン数を“生成級数”という形で整理すると、いろいろな多項式方程式を解く手がかりが出てくるのです。
この整理のしかたを拡張すると、2次や3次だけでなく、どんな次数の方程式についても同じように対応できるようになる、というのが今回の狙いです。
ある意味で「小さな計算を積み重ねていくことで、大きな答えに近づく」というイメージです。
たとえば円周率の近似を思い浮かべるとわかりやすいかもしれません。
私たちは円周率を精密に知りたければ、「3.1」「3.14」「3.1415」…というふうに、桁数を増やすたびに精度が高まります。
無限に桁を増やし続ければ、理論上は円周率の正確な値にたどり着くのと同じです。
今回の方法は、この“桁を増やす”というイメージを、多項式方程式の解を見つける作業に応用していると考えてください。
そして「積み上げる項数を増やせば増やすほど、解がより正確になる」という仕組みを理論的に保証できれば、次数が2だろうと5だろうと、最終的には正しい解に近づけるはずだというわけです。
たとえば一般的な産業用途では、およそ小数点以下5桁から6桁程度の精度があれば十分とされるケースが多いようです。
さらに先端的な精密機器や科学実験の世界に行くと、小数点以下10桁以上の精度を要求されることもしばしばあります。
こうした現場の“必要精度”は、実際に機械や実験がどの程度の誤差を許容できるかによって変動しますが、少なくとも「少数の数桁をきちんと合わせる」ことはほとんどの実用分野で不可欠といえます。
このような数桁から10桁クラスの精度なら、今回紹介した“無限級数を使った解法”でも、足す項数を少し増やすだけで十分に得られる可能性があります。
さらにこの過程からは、これまで知られていなかった「ジオード(Geode)」という新しい配列も見つかりました。
多角形を区切った面を数えるように項を積み上げていくと、大きな級数が不思議な形で“因数分解”されるのですが、その因数分解先が「ジオード配列」という、カタラン数をさらに下支えするような構造になっていたのです。
ワイルドバーガー教授は「ジオード配列はまったく新しい発見で、カタラン数を一段と拡張したようなものだ」と話し、これから数多くの新たな課題が生まれるだろうと期待を寄せています。
実際、ワイルドバーガーは今回の級数解法を使って式を十分な項まで計算(切り上げ)し、既知の例で正しい数値解が得られることを確かめています。
例えば、17世紀の数学者ジョン・ウォリスが示した有名な3次方程式でこの方法を試したところ、解が見事に導けたと報告されています。
研究者たちは「5次方程式(クインティック)ですら解が得られる」とも述べており、これまで「不可能」と見なされてきた領域にも新たな光が差し込んでいることがうかがえます。
ルートに頼らない代数学――計算機アルゴリズムはどう変わる?
今回の研究成果が意味するところは、「高次方程式を一貫した手法で解く方法が見つかった」というだけではありません。
むしろ、これまで当たり前に使ってきた“無理数”や“無限”の概念に固執しなくても、具体的な図形や組み合わせの数え上げを手がかりに、新しい計算の仕方を組み立てられるという可能性を示しているのです。
たとえば正多角形をいくつかの多角形に分割する、というとてもイメージしやすい方法を通じて、多項式方程式のような一見抽象的な問題を初心者でも視覚的に理解しやすくなります。
さらに実用面でも、コンピュータに方程式を解かせる際にこれまで当然のように用いてきた「無理数(√のようなルート計算)」を、段階的に加算していく級数ベースの方法に置き換えられるなら、新たなアルゴリズムやより高精度な計算手法が生み出される可能性があります。
かつては絶対に開けないとされていた“5次方程式”という門戸が、いまや新しい考え方でこじ開けられようとしているのです。
古くから「ここで終わり」と思われていた数学の章が、実はまだ書き換え可能だったとわかり、多くの研究者が今後どのようにこの理論が応用されていくのかを注目しています。
参考文献
Radical rejection behind new method
https://www.unsw.edu.au/newsroom/news/2025/05/mathematician-solves-algebras-oldest-problem-using-intriguing-new-number-sequences#:~:text=A%20UNSW%20mathematician%20has%20discovered%20a%20new%20method,4%20x%20-%203%20x%202%20%3D%200.
元論文
A Hyper-Catalan Series Solution to Polynomial Equations, and the Geode
https://doi.org/10.1080/00029890.2025.2460966
ライター
川勝康弘: ナゾロジー副編集長。 大学で研究生活を送ること10年と少し。 小説家としての活動履歴あり。 専門は生物学ですが、量子力学・社会学・医学・薬学なども担当します。 日々の記事作成は可能な限り、一次資料たる論文を元にするよう心がけています。 夢は最新科学をまとめて小学生用に本にすること。
編集者
ナゾロジー 編集部