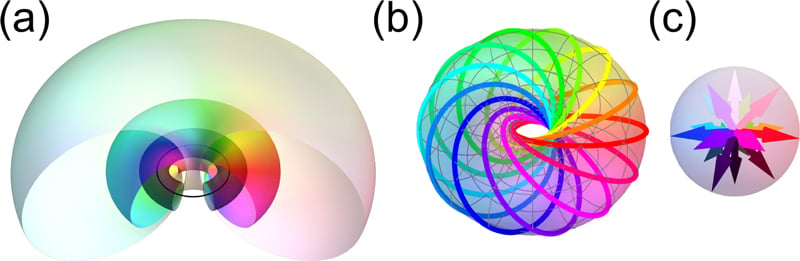
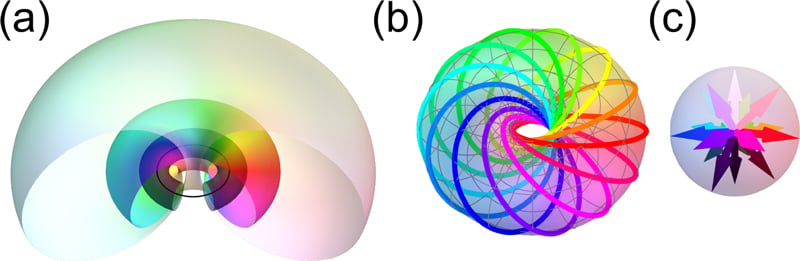
日本の東京科学大学や東京大学、慶応大学、シンガポール南洋理工大学など国際研究チームによって、光をまるで「ひも」のように三次元的に結び合わせることで、空間だけでなく時間の中でも同じパターンが繰り返し現れる「光の結び目の結晶構造(ホプフィオン結晶)」が理論的に作り出されました。
このホプフィオン結晶は、結び目のように安定した光のパターンに情報を「縛り付ける」ことにより、情報を崩れにくく高密度に保存・伝送できる可能性があります。
実現すれば、次世代の超高速通信や超安定な情報保存技術が誕生するかもしれません。
この不思議な光の結び目とは一体どのような仕組みで生まれたのでしょうか?
(※結晶の基礎的な説明などは不要という人は最終ページに飛んで下さい)
研究内容の詳細は2025年8月21日に『Physical Review Letters』にて発表されました。
目次
- 光の「結び目」が次世代通信を変える
- 光を三次元に結びつける「ホプフィオン結晶」
- ホプフィオン結晶の誕生が与えるインパクト
- やや詳しい解説(専門家向け)
光の「結び目」が次世代通信を変える
私たちが暮らす日常には、さまざまな「形」があふれています。
その中には、見た目は全然違うけれど、「本質的には同じ」と考えられるものがあります。
例えば、ドーナツとマグカップを思い浮かべてみましょう。
ドーナツは丸い穴が中央に空いていて、マグカップには取っ手の部分に穴がありますね。
一見するとまったく異なる二つの形ですが、実はどちらも「穴がひとつだけ」という共通点を持っています。
柔らかい粘土で作られているとしたら、マグカップをぐにゃぐにゃと変形させてドーナツの形にすることもできます。
このとき、穴の数は変わらないので、「同じ形」と見なされます。
このように、形をぐにゃっと自由に変形しても変わらない性質を数学的に調べる学問があります。
それがトポロジー(位相幾何学)と呼ばれる分野です。
トポロジーをざっくり言うと、「形の細かな違いは無視して、穴の数や絡まり方といった『大まかな特徴』だけに注目する数学」なのです。
トポロジーの考え方は「結び目」を理解する上でも役立ちます。
紐をぎゅっと結ぶと、その絡まり方は、紐を切ったりほどいたりしない限り変わりませんよね。
結び目には、少々引っ張ったり押したりしても簡単にはほどけない安定性(丈夫さ)があります。
こうしたトポロジカルな結び目の丈夫さは、最新の情報技術に活かせるかもしれないと注目されてきました。
なぜなら、結び目の丈夫さを使えば、情報を安全かつ確実に記録したり送ったりできる可能性があるからです。
そんなトポロジカルな構造の中で、特に期待を集めているのが「ホプフィオン」という存在です。
ホプフィオンとは、粒子のように空間の中に存在する3次元の結び目状の構造で、ドーナツの形をした輪っか(トーラス)に糸が巻き付いたような複雑なパターンをしています。
ホプフィオンを分かりやすくイメージするには、毛糸玉を想像してみてください。
毛糸玉の中には一本の糸が複雑に絡み合っていますが、ホプフィオンも似たように、見えない「糸のような線」が内部でループ状に複雑に絡まりあっている構造なのです。
この絡まり方は、ほどくことなく変形させても変わらないので、安定した情報の記録に向いていると考えられています。
実際、ホプフィオンはごく最近になって、磁石のような性質を持つ物質(磁性体)の中や、光の中に孤立した「単体」として見つかりはじめました。
こうした発見をきっかけに、「ホプフィオンは非常に丈夫で、情報を高密度で安定に保存したり運んだりする新しい方法になるのではないか?」と期待されるようになったのです。
ですが、これまでに見つかったホプフィオンはどれも「孤立した状態」で、規則正しく並んだ「結晶のようなホプフィオン」はまだ見つかっていませんでした。
もし、ホプフィオンがきれいに並んだ「ホプフィオン結晶」を作ることができれば、その研究はホプフィオンそのものの性質を深く理解するための大きな発見になるはずです。
それだけでなく、トポロジーを使った次世代の通信技術や超高密度な情報保存技術への扉も開かれるでしょう。
こうした可能性を秘めたホプフィオン結晶ですが、その実現は決して簡単ではありませんでした。
そこで今回、東京工業大学・東京大学・慶應義塾大学・南洋理工大学(シンガポール)からなる国際研究チームが、この大きな課題に挑戦したのです。
研究チームが目指したのは、光を使ってホプフィオン結晶を理論的に作り出すことでした。
光を使う理由は、光が情報を速く、遠くまで届けられる特性を持つからです。
研究者たちは、2つの違う波長(色)をもつ光をうまく重ね合わせて「ビート(拍)」という周期的な波を作り出すことにしました。
光には波の向きを示す「偏光」という性質があり、この偏光が時間的に繰り返す「拍」を使えば、時間方向に規則的に並んだホプフィオンの構造を作れるのではないかと考えたのです。
さらに彼らは、たくさんの小さな光の発光源を規則正しく並べて、その光が遠く離れた場所で重なり合うことで、空間方向にも繰り返す格子模様を作るアイデアを考案しました。
これにより、ホプフィオンが空間方向と時間方向の両方で規則正しく並ぶような「光の結び目結晶」を理論的に設計しようとしたのです。
つまり研究チームの最終目的は、ホプフィオンという「光の結び目」を、四次元(空間3次元+時間)という広い舞台に、規則正しく編み込んでいく新たな方法を見つけることだったのです。
光を三次元に結びつける「ホプフィオン結晶」
研究チームはまず、「ホプフィオンの結晶を作る」という大きな目標に向かって、段階的な研究を進めました。
最初のステップとして、ホプフィオンを「時間方向に並べる方法」を探ることから始めました。
ここで重要なのが「光の性質」です。
光には波の性質があり、水面に投げ入れた2つの小石が作る波紋が重なり合って模様を作るように、2つの光を重ね合わせることで特別な波のパターンを作れます。
研究チームは、この性質を利用して、少しだけ波長(光の色)が異なる二種類の光を重ね合わせました。
すると、この重なった光には「うなり(ビート)」と呼ばれる、周期的に強くなったり弱くなったりする性質が現れます。
研究者たちはさらに、光のもう一つの重要な性質である「偏光」を利用しました。
偏光とは、簡単にいうと「光が波としてどちら向きに振動しているか」という光の向きの情報です。
例えば、ロープを持って上下左右に波打たせることを想像すると分かりやすいでしょう。
この偏光をうまく調整すると、光が「結び目」のような複雑なパターンを作ることができます。
そこで研究チームは、この「偏光の結び目」が、同じ場所で時間が経つごとに周期的に現れるような条件を注意深く設計し、コンピューター上でシミュレーションしました。
このシミュレーションの結果、同じ位置で時間が進むごとに、規則正しく結び目が繰り返し出現するような状況を実際に確認することができました。
それはまるで、1つ1つのビーズ玉のような「ホプフィオンの結び目」が、一定の時間間隔で糸に通されて連なっているような光の状態でした。
研究チームはこの状態を「一次元ホプフィオン鎖」と呼びました。
このようにして得られた一次元のホプフィオン鎖が、本当に「ホプフィオン」であるかどうかを確かめるため、数学的なチェックを行いました。
ホプフィオンには「ホップ数」と呼ばれる、絡まり方の強さを示す特徴的な数値があります。
この数値は、ホプフィオンが「本物」であるかどうかの指標になります。
研究チームのシミュレーション結果を詳しく調べると、このホップ数がきちんと現れていることが確認されました。
つまり、時間方向に周期的に並ぶホプフィオン鎖を理論的に作り出すことに成功したのです。
次のステップとして、研究者たちはこの鎖を「三次元の結晶構造」に発展させることを考えました。
一次元の鎖はあくまで時間方向だけに周期性を持つものでしたが、本格的な結晶を作るためには、空間方向にも規則的な繰り返し構造が必要です。
そこで研究チームは、複数の小さな光源(発光素子)を規則的に並べ、それらが放つ光が「遠く離れた場所」で重なり合い、空間的に規則的な模様を作り出す仕組みを考案しました。
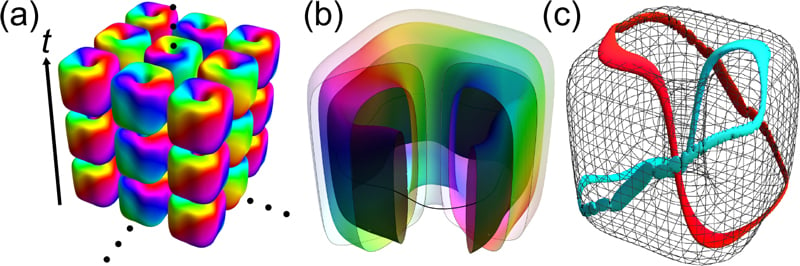
このアイデアをもとに、空間と時間の両方で規則的なパターンを持つ「三次元ホプフィオン結晶」の理論モデルを作りました。
シミュレーションを行った結果、この三次元的に規則正しく並んだホプフィオン結晶の状態を再現することに成功しました。
これは、単に時間方向に並べるだけでなく、空間方向にも規則的な格子状の配列を持つことから、研究チームが目指した「完全なホプフィオン結晶」の理論的な実現につながったのです。
このような三次元ホプフィオン結晶の理論的な設計とシミュレーションによる実証は、世界でも初めての画期的な成果となりました。
さらに、このホプフィオン結晶が特に重要なのは、光が真空のような自由空間を伝わる状態でも作り出せると理論的に示したことです。
通常、物質の中でしか観察できなかったトポロジカルな構造を、物質を使わず「光だけ」で作る可能性を開いたのです。
この研究成果によって、「光を使ったホプフィオン結晶」という新しい分野が誕生しました。
それは、光の中に安定して情報を記録し、運ぶための、まったく新しい方法の第一歩となったのです。
ホプフィオン結晶の誕生が与えるインパクト
今回の研究成果がもつ科学的・技術的な意義は非常に大きく、その意味をより深く理解するために、まず簡単におさらいをしましょう。
この研究の大きなテーマは、光の中に「結び目のような丈夫な構造」を作り、それを規則正しく並べることでした。
結び目の構造を作ることで、情報を安全かつ高密度に保存・伝送できる可能性が生まれるからです。
ではなぜ、結び目を使うことが情報の保存にとって有利なのでしょうか?
実は、結び目のように複雑に絡まった形状というのは、少しくらい引っ張ったり、押したりしても簡単には崩れない安定性があります。
この「形そのものが情報を守る」という考え方を応用すると、光の中に結び目のような構造を作ることで、安定して情報を保存したり伝えたりできると考えられているのです。
今回の研究チームは、こうした理論的な可能性を具体的なシミュレーションで示したことで、「光を結び目状に編んで情報を守る仕組み」の現実味を高めました。
さらに、この成果は、トポロジーという数学を使った新しい情報技術の可能性を一気に広げました。
トポロジーとは、見た目が違っても穴の数や絡まり方が同じであれば同じものとみなす数学のことです。
こうした数学的な仕組みを利用して作られた「ホプフィオン結晶」は、光が空間と時間の両方で規則的に結び目構造を持つことから、「時空に刻まれた情報の格子」と呼べるでしょう。
この新しい格子構造を利用することで、より精密な計測が可能になるだけでなく、光と物質がこれまでにない新しい形で相互作用する現象も発見される可能性があります。
特に注目されている応用の一つが、次世代の通信や情報技術への活用です。
現代の社会は大量の情報を素早く正確に届けることが求められますが、そのためには今まで以上に効率よく情報を送れる方法が必要です。
ホプフィオン結晶は、光の中に「丈夫な結び目」を作ることで、従来より高密度かつ多次元的な情報を記録・符号化できる可能性を秘めています。
これが実現すれば、同じ時間でより多くのデータを送ることが可能になり、さらに結び目構造の丈夫さによってデータの信頼性も向上すると期待されています。
わかりやすく例えるなら、情報を「丈夫なロープで結びつけて安全に届ける」ようなイメージです。
しかし、この夢のような話がすぐに現実になるわけではありません。
今回の研究はあくまでも理論的な設計とシミュレーションによる検証段階にあり、実際に実験で確かめることが次の大きな課題となっています。
現実の光の中にホプフィオン結晶を作り出し、それを実際に観察するのは決して簡単ではないでしょう。
ですが、研究チームが今回示した理論設計は、ホプフィオンという新しい情報担体の可能性を広げる重要な第一歩となりました。
さらに、この成果によって、ホプフィオンを探求する研究がさらに広がることも期待されます。
例えば、光以外の電磁波(電波やマイクロ波など)や音波、さらには磁性体など物質の中でも、ホプフィオン結晶が見つかるかもしれません。
この研究がきっかけとなって、さまざまな物理的な環境でホプフィオンの探求が進むことで、通信や情報保存技術の可能性はさらに広がるでしょう。
やや詳しい解説(専門家向け)
技術的背景と前提
本研究は、2色の構造化光から得られる時間変調された偏光を擬似スピン(pseudospin)として扱い、(x, y, t) の時空(z=0 のビームウエスト面)上にホプフィオン結晶(時間周期の1D鎖、さらに空間×時間周期の3D結晶)を設計・数値実証したものです。従来の「伝搬軸 z に沿う回折・Gouy 位相の利用」による光学ホプフィオン生成とは異なり、設計の主舞台を z=0 の1枚の面(spatiotemporal domain)に固定し、二色ビート(bichromatic beating)を主役に据えています。結果として、回折に依存しないトポロジカル設計指針が提示されます。
擬スピン場の定義(2色光)
2つの波長 λ1, λ2 をもつ電場を重ねた全電場を E(t) とし、偏光の時間変化を擬スピン s(t) に写像します。擬スピンは正規化ストークス・ベクトルの拡張として
s(t) = (sx, sy, sz)
sx = [E*(t) sigma3 E(t)] / [E*(t) E(t)]
sy = [E*(t) sigma1 E(t)] / [E*(t) E(t)]
sz = [E*(t) sigma2 E(t)] / [E*(t) E(t)]
で定義されます(sigma1, sigma2, sigma3 は Pauli 行列)。二色の波長比が有理数のとき、E(t) は時間に対してビート周期を持ち、擬スピンは周期的に閉じた軌跡(Lissajous 的)を描きます。波長差が小さい極限では、s(t) は瞬時ストークスに近似されます。
1D 時空ホプフィオン結晶(基本設計)
横断面 (x, y) と時間 t で完結する1周期セル内に、ホプフィオンの境界条件(中心と無限遠で spin-up、内部に spin-down の輪)を満たすよう、円偏光の 2成分に異なる空間モードを割り当てます。最も基本の P=1 構成は概略
E(r, t) =
[ LG00(r,t|λ1) + LG01(r,t|λ2) ] * e_L
+ [ LG10(r,t|λ1) – LG10(r,t|λ2) ] * e_R
(r=(x,y), e_L/e_R は左/右円偏光の単位ベクトル)。
LG00 と LG01 の半径方向での位相反転により強度ゼロのリング(spin-down 円)が形成され、他方成分の LG10 を対に配置することで時間軸上の境界条件(瞬間的な一様 spin-up)を実現します。これにより、等方位線(isospin lines)がトーラス上の閉曲線をなす 3D 結び目構造が1周期ごとに現れます。Hopf 密度を体積積分して得られるHopf 数 Q_Hは基礎例でほぼ整数(≈ ±1)です。
高次化と符号反転(設計つまみ)
ホプフィオンの Hopf 数は Q_H = P × Q(P は (x,y) 面の巻き数、Q は (x,t) 面の巻き数)で与えられます。本論文では主として P の制御を示し、任意の整数 Pを持つセルを合成します。鍵は、LG0p を重み付きで重ねて半径多項式 r^(2pm) − r0^(2pm) を合成することです。代表的な構成は
W1(r,t|λ) = sum_{p=0..pm} [ (-1)^p / (pm! (pm-p)! p!) ] * LG0p(r,t|λ)
W2(r,t|λ) = [ (2 r0^2 / w0^2)^pm / pm! ] * LG00(r,t|λ)
を用い、
E(r,t) = [ W1(r,t|λ1) – W2(r,t|λ2) ] * e_L
+ [ LG_l0(r,t|λ1) + LG_l0(r,t|λ2) ] * e_R
とすると P = l(l は方位次数)を実現できます。数値例として P=2,3 では、Hopf 密度積分から Q_H = −2, −3 が得られています。さらに、二色の波長を入れ替えるだけで Q_H の符号反転が可能です(Q の詳細制御は P より難しいが、符号操作は容易)。
3D 時空ホプフィオン結晶(遠方界での合成)
遠方界(far field)で格子状の擬スピン場を作るため、点状の放射源アレイ(双極子)を二色・二偏光で駆動する設計が示されています。概略は次の通りです。
- まず 1 波長あたり 16 個の周辺ソース(+ 中央 1 個の計 17)で、スキルミオニウム格子を遠方界に合成(右円偏光側で OAM±1 の格子、左円偏光側で OAM なし・各セルに閉曲線ゼロ強度)。
- これを2色に拡張して時間ビートを与え、さらに中央の左円偏光ソースを逆位相ビートで重ねると、一様 spin-upの瞬間とスキルミオニウム出現の瞬間が交互に現れ、3D(空間×時間)ホプフィオン結晶が得られます。
- 遠方界の格子定数一致のため、各ソースの相対位置は波長に比例スケーリングが必要です。
得られる単位スーパーセルは4つのサブセルからなり、スキルミオニウム/反スキルミオニウムが交互に配置されます。Hopf 密度は**+1 と −1 が交互に出現し、交互トポロジーが実現します。補足では、1 波長あたり 17 ソース(理想的には二色で位置がわずかにずれるため計 33 位置**)の配置表・複素振幅・偏光が具体に提示されています。
トポロジカル評価(Hopf 密度と不変量)
擬スピン場 s(x,y,ζ)(ζ=ct)から擬磁場 F とベクトルポテンシャル A を定義し、Hopf 密度 ρ_H = F · A を積分して Q_H を得ます。
Q_H = (1 / (4 pi)^2) ∫∫∫ F · A dx dy dζ
F_i = (1/2) * epsilon_ijk * [ s · (partial_j s cross partial_k s) ]
curl A = F
ゲージに依存して ρ_H の形は変わり得ますが、体積積分 Q_H はゲージ不変です。計算は空間・時間の 3D フーリエ空間で curl A = F を解く形で実装されています。
伝搬(“飛ぶ”条件)と設計上の留意点
本研究の時空設計はz=0 面で議論されていますが、ビートによる包絡変調が回折拡がりを上回る設計条件では、ホプフィオン列が有限距離を伝搬しつつ Q_H を保持することが数値的に示されています。Rayleigh 長が「格子の空間周期」より十分大きいときは Q_H が理想値に近い一方、同程度以下に短くなると負の Hopf 密度が混入し、Q_H は理想値から劣化します。すなわち、Rayleigh 長 >> 周期が安定伝搬の目安です。
既存アプローチとの差分
- 回折・Gouy 位相を意図的に活用して z 方向で構造を組む先行法に対し、本設計はz=0 面の時空干渉(2色ビート)で局所的に 3D トポロジーを実現。
- 高次 Hopf 数の系統設計(P の任意整数化と符号反転)が、LG モードの合成と二色パラメタの切替だけで与えられる。
- 遠方界アレイという実装指向の具体設計(ソース配置・偏光・位相・スケーリング条件)が提示されている。
数値設定の代表例(再現の足がかり)
- 二色比の一例:λ1 = 1 μm, λ2 = 1/1.01 μm(ビート長 ct = 100 μm 例)。
- ビーム腰半径:10 μm(z=0)。
- 高次例:P = 2, 3 で Q_H = −2, −3。
- 補足の“飛行”例:条件良好では 5 周期合算で Q_H ≈ 4.98、条件不良では ≈ 3.5。
- 3D 結晶:理想的には 1 波長あたり 17 ソース、二色で 33 位置(近接波長なら近似して簡素化可)。
想定される適用レンジと限界
本稿は理論・数値設計であり、実験的生成や雑音・誤差への堅牢性評価は未実施です。周波数帯(光・テラヘルツ・マイクロ波)への拡張可能性は示唆されますが、実装の具体化はデバイス(例:双極子アンテナ配列、マイクロアンテナ、SLM 等)の工程設計に依存します。Q の自在制御は P に比べて難度が高く、符号操作は容易であるものの、完全な任意制御に向けた最短経路は今後の課題として残ります。
参考文献
空飛ぶホプフィオンの3次元周期構造を発見―高密度・超安定な情報の担い手―
https://www.rcast.u-tokyo.ac.jp/ja/news/release/20250822.html
元論文
Space-Time Optical Hopfion Crystals
https://doi.org/10.1103/hh5s-cprt
ライター
川勝康弘: ナゾロジー副編集長。 大学で研究生活を送ること10年と少し。 小説家としての活動履歴あり。 専門は生物学ですが、量子力学・社会学・医学・薬学なども担当します。 日々の記事作成は可能な限り、一次資料たる論文を元にするよう心がけています。 夢は最新科学をまとめて小学生用に本にすること。
編集者
ナゾロジー 編集部