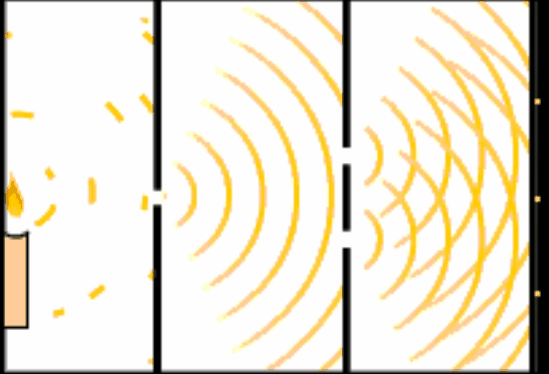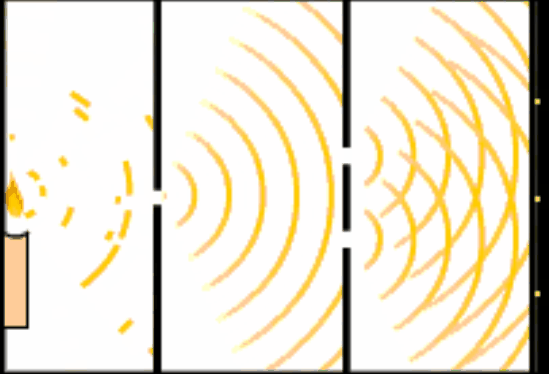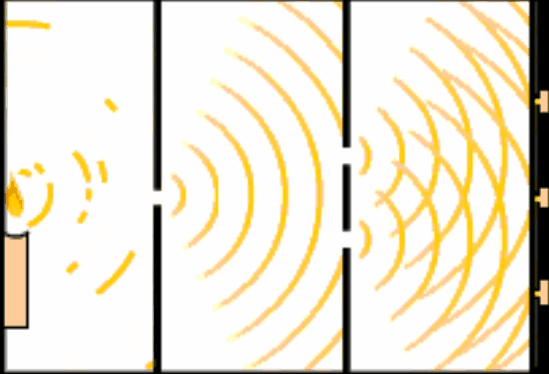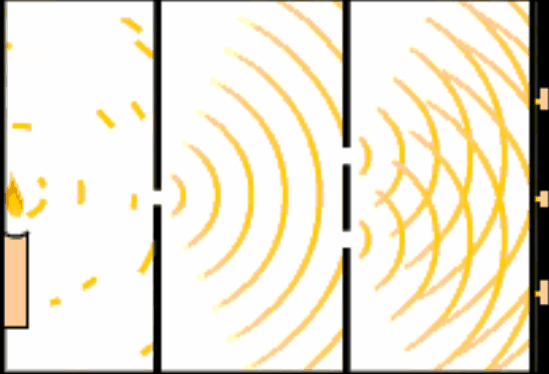
アメリカのマサチューセッツ工科大学(MIT)で行われた研究により、有名な「二重スリット実験」の「本質」を極限までシンプルにすると、物質の“もやもや”した存在確率、つまり量子の特徴そのものだけで成り立つことが、今回の最新研究ではっきり示されました。
この実験では、通常のように板に空いた二つの穴(スリット)を使うのではなく、代わりに“ぼんやりした位置”に存在する原子そのものをスリットとして使いました。
原子の位置は完全には決まっておらず、「このあたりにいる確率が高い」という、いわゆる“波束(はそく)”という形で広がっています。
そんな原子のそばに1個の光子を飛ばすと、光子は原子のどこかをかすめて通ります。
その際、光子が原子にほんのわずかな影響を与えることで、「どちらを通ったか」という情報がこの世界のどこかに記録されてしまいます。
するとその瞬間、光は“波”としてのふるまいをやめ、“粒”として観測されるのです。
この極限までシンプルにした「原子×光子」の実験でも、「情報の記録が現実を変える」という量子のルールがそのまま働いていることが確認されました。
つまり、重たい観察装置や大がかりなスリット板がなくても、たった一つの原子と光子だけで、量子力学が示す「観察=情報の記録が現実に影響する」ことが実証されたのです。
(※論文の厳密な解説のみが読みたいというひとは最終ページに飛んで下さい)
研究内容の詳細は2025年7月22日に『Physical Review Letters』にて発表されました。
目次
- アインシュタインが残した二重スリット実験の宿題
- スリットの代りを「1個の原子」に任せる究極の簡素化
- 二重スリット実験で「アインシュタインの宿題」を解決した
- ややくわしい解説
アインシュタインが残した二重スリット実験の宿題
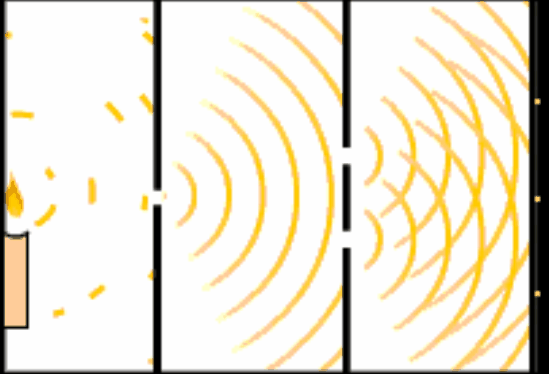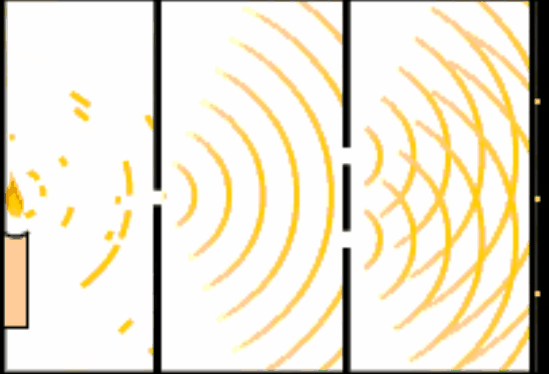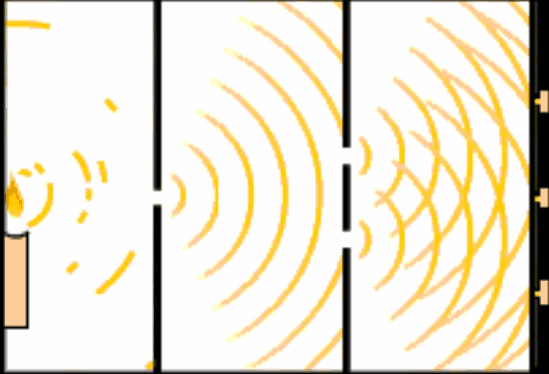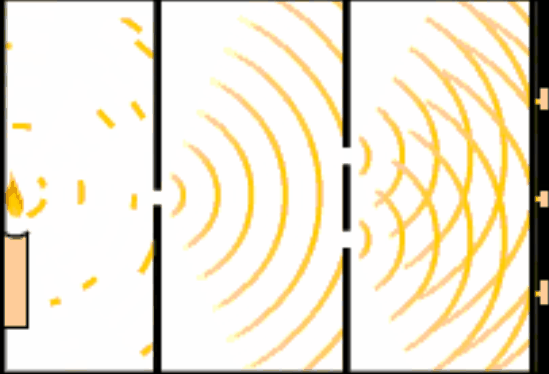
光が波なのか粒なのか――これは量子力学の出発点ともいえる問いです。
その答えを探るために考案されたのが、あの有名な「二重スリット実験」です。
まずは、日常的な例で考えてみましょう。
砂粒やBB弾のような粒を、2つの穴を通して奥のスクリーンに向かって飛ばすと、それぞれの穴の位置に対応した2本の線がスクリーンに現れます。
これは当然の結果です。ところが光で同じことをすると、まるで水面の波のように広がって、2つの穴の後ろに明るい線と暗い線が交互に並ぶ「干渉縞(かんしょうじま)」が現れます。これは「波の性質」が働いている証拠です。
けれども、その光が「どちらの穴を通ったか」を調べるために観察装置を設置すると、あのしま模様は消えてしまい、光は粒のようなふるまいだけを見せるのです。
つまり光は、「粒」としての性質と「波」としての性質を持ちますが、それらは同時には現れてくれません。
このようなふるまいを説明する考え方が「相補性原理(そうほせいげんり)」であり、量子力学の核心的な原理の一つとなっています。
しかし、20世紀初頭の物理学者アルベルト・アインシュタインは、この現象に疑問を抱いていました。
彼は「観察によって現実が変わる」という量子力学の考え方には懐疑的で、「実際の世界は、私たちが見ようが見まいが、ちゃんと存在している」と信じていたのです
そこで1927年に、アインシュタインはあるアイデアを提案しました。
光が本当に「粒」であるならば、粒がスリットを通る瞬間にスリットをわずかに揺らし、微かな反動を与えるだろうと考えました。
例えば、小鳥が木の葉にぶつかったときに葉がわずかに動くような感じです。
もしスリットがバネのような非常に敏感な装置で支えられていれば、光が通過する瞬間の微妙な揺れを検知できるはずです。
つまり、粒子として光の経路を特定できることになります。
一方で、光が波としての性質を同時に示し、スクリーンにしま模様(干渉縞)も現れるならば、光の「粒」と「波」の両方を一度に観察できる可能性があります。
アインシュタインは、このように極めて繊細な観察を行えば観察による影響は限りなく小さくなり、実験の前半では光が粒子で後半では波として記録され粒子と波の性質が両方同時に見えるかもしれないと考えました。
つまりアインシュタインは、「観察することで現実が変わる」という量子の奇妙な考え方に反論し、「本当にうまくやれば波と粒を同時に見られるのでは?」と主張したのです。
MITの研究チームは、この長年の議論に決着をつけるために、新しい実験を行いました。
果たしてアインシュタインの宿題は果たせたのでしょうか?
スリットの代りを「1個の原子」に任せる究極の簡素化

二重スリット実験のポイントは、光が「波としての性質(干渉縞)」と「粒としての性質(通った道筋の情報)」の両方を同時に示せないというところにあります。
実はこの実験では、スリットをわざわざ穴のあいた板にする必要はありません。
重要なのは、「光が通る2つの位置」があり、そこを通過する光が後で互いに干渉できるような仕組みがあれば良いのです。
つまり、「スリット」は実際の穴ではなくても、光と相互作用する(反応する)物体が適切な位置にあればスリットの役割を果たせるということです。
MITの研究チームは、この点に注目して、スリットを「原子」という非常に小さい粒で作るという新しいアイデアを使いました。
しかし、普通の状態の原子を使っても実験にはなりません。
常温の原子は非常に速く動き回っていて、決まった位置にとどまっていることができないからです。
そこで研究者たちは、レーザー光線を使って約3万個の原子を超低温(絶対零度に近い非常に冷たい温度)まで冷やしました。
この超低温状態では、原子はほとんど動きを止め、氷の中に閉じ込められたようにその場で止まります。
つまり3万個の原子を用意して、3万個のスリットとして機能させようというわけです。
研究チームのケターレ教授は、これらを「作りうる限り最小のスリット」と呼んでいます。
こうして「究極の二重スリット実験」を、多数の原子(スリットの代替品)を使って実現できるようにしたのです。
実験では、この原子のスリット群に、非常に弱いレーザー光を当てました。
このレーザーは非常に弱く調整されていて、原子一個あたりが同時に複数の光子を散乱することはほとんど起きません。
つまり、一度に散乱される光子(光の粒)は極めて少なく、原子が光子の通った道をはっきりと記録できるかどうかを精密に調べることができました。
また、研究者たちは原子の固定の強さを制御することで「はっきりと固定された状態(存在確率の範囲が狭い)」と「ぼんやり広がった状態(存在確率の範囲が広い)」という二つの状態を作り、その違いが光の振る舞いにどう影響するかを調べました。
このときレーザーを強くして原子をはっきり固定すると、原子は光子が通った道の情報をほとんど記録できなくなります。
原子自身が全然“もやもや”していないので、光子に「道の痕跡」を残してもらう場所がほとんどないからです。
こうなると光子は量子的な波のような性質を強く示し、はっきりとした干渉縞が見えます。
逆に、原子が「もやもや」と広がった存在確率(波束)を持っている場合、原子が「自分のどこを通ったか」を光子とのやりとりで“記録”しやすくなります。
原子が広がっていれば広がっているほど、光子が通ると原子のどこかに「足跡」をつけることができ、その情報が残ります。
その結果、量子的な波の性質が消えてしまい、光は粒子として振る舞ってしまいます。
この「情報の記録」こそが、量子の“波のような重ね合わせ”を壊してしまうスイッチなのです。
コラム:なぜ情報の記録が量子的性質を奪うのか?
量子力学では、光子はスリットを通るときに「どっちの道も同時に通る(波の重ね合わせ)」という状態になっています。でも、スリット(や原子)がその通り道を“感じ取り”、その情報が(たとえば原子の動きやエネルギーの変化として)残ってしまうと、「光子がAを通った」と「光子がBを通った」という2つの世界が、もう互いに“混ざることができなくなる”のです。これは“エンタングルメント(量子的なつながり)”という現象とも深く関係しています。光子と原子が一瞬「つながった」ことで、どちらの道を通ったかという情報がどこかに“書き込まれる”と、もはや両方の道を同時に進むことはできなくなり、波としての性質(干渉)は消えてしまうのです。逆に言えば、情報がどこにも残っていなければ、「どっちも通った」状態のまま、波としてふるまうことができるのです。要するに――「観察=情報の記録や確定」こそが、“波と粒の分かれ道”を作るスイッチです。これは、誰かが実際に目で見たかどうかは関係なく、“物理的に世界のどこかに情報が刻まれた瞬間”に現実のあり方が変わる、というのが量子のルールなのです。
さらに研究チームは、アインシュタインが提案した「バネ仕掛けのように繊細にスリットを支える装置」が本当に必要なのかも確認しました。
具体的には、原子を固定していたレーザーを突然オフにして、原子が自由に浮遊するような状態でも実験を行いました。
もしアインシュタインの考えが正しければ、原子が固定されていない状態では結果に変化が起こるはずでした。
しかし実験結果は、固定された状態でも自由な状態でもまったく同じでした。
つまり、バネのような仕掛けは重要ではなく、「原子がどれだけぼんやりと位置が広がっているか(位置の不確かさ)」が唯一、光の振る舞いを決定する要素だったのです。
研究者たちは「バネのような仕掛けではなく、原子自身の『ぼんやり度』(位置の広がり)が本質的に重要だ」と述べています。
また論文でも、この結果を数学的な理論で明確に示しています。
この実験によって、量子力学の基本的なルールが極限まで理想的な条件でも正しいことが実証されました。
実験データはすべて、このシンプルで美しいルールにぴったりと一致したのです。
二重スリット実験で「アインシュタインの宿題」を解決した

今回の研究で特に重要だったのは、「光が粒として振る舞うか、波として振る舞うかを決めるのは、原子の位置がどれだけはっきり決まっているか、あるいはぼんやりと広がっているか」ということをはっきりと確認できたことです。
原子や電子などの量子の世界にある非常に小さい粒子は、位置がはっきりしない「ぼんやりした状態」で存在していることがあります。
これを「位置の不確定性」と呼びます。
今回の実験では、原子の位置がはっきり決まっていると、原子が光子(光の粒)の通った道筋の情報を記録することが難しくなり、干渉縞が作られます。
逆に原子の位置がぼんやりと広がっている場合は、原子が光子の通った道筋をはっきり記録できるため、光は粒のように振る舞い、干渉縞は消えてしまいます。
つまり、原子の位置の量子的なぼんやり具合と、光が粒または波として振る舞うかどうかが、きれいに連動しているのです。
これは昔アインシュタインが提唱した、「非常に繊細な装置を使えば、光の粒子としての情報(経路情報)を得ながら、波としての情報(干渉縞)も同時に見ることができるかもしれない」という考え方に関連しています。
しかし今回の実験では、そのような仕組みを使わずに、「原子の位置の不確定性」という量子力学の基本的な性質のみを利用した非常に理想的な条件を作り出しました。
それにもかかわらず、粒としての性質をはっきり観察すると、波としての性質は消えてしまい、逆に波の性質を明確にすると粒子の情報は失われてしまったのです。
この結果は、「粒と波を同時にはっきり観察することは不可能である」という量子力学の予測と完全に一致しました。
さらに研究チームは、原子を固定していたレーザー(アインシュタインが考えたバネの役割を果たす装置)を突然オフにして、原子を完全に自由に浮遊させても実験を行いました。
すると結果には全く変化がなく、バネのような仕掛けがあるかないかは実験の結果に影響しませんでした。
つまり、重要なのは原子を支える仕組みではなく、「原子の位置がどれくらいはっきりしているか、あるいはぼんやりしているか」ということだけだったのです。
研究チームのFedoseev氏もプレスリリースの中で、「バネのような仕掛けは本質ではなく、原子自身の位置のぼんやり具合(位置の広がり)こそが重要だ」と説明しています。
また論文の中でも、原子の位置のぼんやり具合が干渉縞の鮮明さを決めることを数学的に明確に示しました。
この発見は、私たちが世界を理解する方法にも大きな影響を与えます。
なぜなら、量子力学では「観察」という行為そのものが、物理現象の結果に直接影響を与えることが実験的に証明されたからです。
今回の実験では、その影響がどれほど根本的で避けられないものかがはっきりしました。
今後は原子を2つ並べたり、スピン(電子の磁石のような性質)の状態を重ね合わせるなどして、より複雑な条件下で量子の波の性質(コヒーレンス)がどのように失われていくかをさらに詳しく研究する予定です。
こうした研究を通じて、量子の世界のルールがどこまで広く当てはまるのかを明らかにできるかもしれません。
将来的には、こうした基礎的な量子の研究が、量子コンピューターや量子通信といった私たちの未来を変える技術の開発にもつながると期待されています。
(※次ページは論文のやや詳しい解説なのでより厳密に知りたい人だけ読んでください)
ややくわしい解説
本研究は、二準位原子の単一原子波束に対する単一光子のレイリー散乱(弱励起・遠赤 detune・低光学密度)に限定し、干渉可視度の起源を原子波束の空間的広がりに帰着させる理論・実験の統合検証である。
理論は、二つの原子波束を「最小のスリット」に見立て(解析自体は単一原子にも落とせるが、説明の便宜上2原子干渉で提示)、弾性・コヒーレント散乱のみが干渉に寄与するという出発点から、有限コントラストの源が光‐原子の部分的エンタングルメントにより付与されるwhich-way情報であることを明示する。
実験射程は「最も単純な状況」、すなわち二準位+弱励起+遠赤 detuneの単純レイリー散乱極限に厳格に制限されている。
光子モードの密度演算子は、原子自由度を部分トレースすることで、コヒーレント成分とインコヒーレント成分の混合として厳密に与えられる。
記号は本文と同様に用いる(|0>, |1> は光子数状態、γ1,γ2 は散乱位相、β は変位演算子の行列表現、ε は小さな励起振幅)とすると、
ρ_photon
= ( |0> + ε <0|β> (γ1 + γ2) |1> )
( <0| + ε* <β|0> (γ1* + γ2*) <1| )
+ 2 |ε|^2 ( 1 – |<β|0>|^2 ) |1><1| .
このとき
D ≡ |<β|0>|^2 = | < exp(i Q·R) > |^2 = exp( – η^2 ), η ≡ Q x0 ,
で定義されるDebye–Waller 因子 Dがコヒーレント分率を与え、インコヒーレント分率は f_incoh = 1 – D となる。
2原子の場合、コヒーレントな干渉項の光子数は |ε|^2 D |γ1+γ2|^2、インコヒーレントは 2 |ε|^2 (1-D) で与えられる(単一原子ならそれぞれ |ε|^2 D と |ε|^2 (1-D))。これらは格子の有無(捕捉ポテンシャルの存在)に依存しない一般則として導かれ、モスバウアー的な担体線・側帯の分離や再加熱の有無は分率の決定因子ではない。
物理的本質は光と原子の部分的エンタングルメントであり、古典的振動子アレイの散乱(純コヒーレント)とは本質的に異なる。
実験は、Li-7 と Dy-162 で単一占有の Mott 絶縁相を形成し(それぞれ ~3×10^4 原子規模)、Bragg 角から外れた散乱角で検出することにより、測定強度
I(Q) = D · S(Q) + f_incoh
の形で構造因子 S(Q) とインコヒーレント分 f_incohを分離できる配置を採用した。格子スイッチオフは 0.1 μs 程度で行い、プローブは FWHM 0.1 μs の短パルス(または 4 μs の長パルス)を用いた。
主要結果は三点に要約できる。第一に、格子オン直前とオフ直後での散乱強度 I は実験誤差内で同一であり、コヒーレント/インコヒーレント分率が捕捉の有無に依存しないことを実証した(“trap-free” と“in-trap”の等価性)。
第二に、側帯が分解される長パルスと分解されない短パルスで I は同程度(例:0.48±0.04 vs 0.52±0.04)であり、側帯分解の有無はコヒーレンス特性に影響しない。第三に、コヒーレント光とインコヒーレント光が同一周波数を共有しうることを実測で確認した。
これらは理論の「分率は D だけで決まり、捕捉や側帯の有無には依らない」という帰結と整合する。
自由空間での時間発展については、格子から解放されたガウス波束のrms半径 x(t) = x0 sqrt(1 + (ω t)^2) に対し
D(t) = exp( – Q^2 x(t)^2 )
と減衰し、十分長い time-of-flight では D → 0、したがって f_incoh → 1 に近づく。
Li と Dy の比較では、Dy 系で高い時間分解能の下、格子オフ直後の抑制がオン時と同一であること、および二つの捕捉周波数(例:2π×21 kHz, 2π×43 kHz)での f_incoh(t) がガウス波束の拡散モデルと定量的に整合することが示された。
なお実データの正規化は長時間極限で D<0.01 を満たす条件で f_incoh → 1となるように取られている。
which-way 情報の生成機構は、長パルス in-trapでは励起調和振動子状態への遷移確率(Fermi の黄金律)で直接読み出され、短パルスでは運動量シフトを受けたモーメンタムずらし波束の生成として理解される。
自由空間での which-way の定量化に向け、照射直後に調和ポテンシャルを急投入して占有分布を読めば、エンタングルメントに由来するwhich-way情報(=コヒーレント分率)を投影的に計測できる実験プロトコルも提案されている。
加えて、コヒーレント分率 D は運動量幅に依存せず、空間幅 x0 のみで決まるという一般化が与えられ、その数学的理由は「運動量シフトの生成子が位置演算子である」ことに求められる。
以上より、本研究は「I(Q) = D · S(Q) + (1-D)」という測定可能な形で干渉の可視度を D に因果帰着し、実験的には捕捉の有無・側帯分解の有無・周波数(担体線 vs 同一周波数の散乱)といった装置要素から一般則を切り離して検証した点に本質がある。
結果は、単一不確定性限界波束の散乱において、インコヒーレント散乱は空間的非局在化(= D の低下)に等価であり、その源はエンタングルメントであるという量子記述と首尾一貫している。
将来拡張として、n=2 Mott(2原子波束)やスピン重ね合わせ状態での**相互作用起源の which-way 付与(例:1/R^3 双極子相互作用→radiative escape)**の優勢化が予見され、同一手法でのコヒーレンス劣化の分離同定が提案されている。
参考文献
Famous double-slit experiment holds up when stripped to its quantum essentials
https://news.mit.edu/2025/famous-double-slit-experiment-holds-when-stripped-to-quantum-essentials-0728
元論文
Coherent and Incoherent Light Scattering by Single-Atom Wave Packets
https://doi.org/10.1103/zwhd-1k2t
ライター
川勝康弘: ナゾロジー副編集長。 大学で研究生活を送ること10年と少し。 小説家としての活動履歴あり。 専門は生物学ですが、量子力学・社会学・医学・薬学なども担当します。 日々の記事作成は可能な限り、一次資料たる論文を元にするよう心がけています。 夢は最新科学をまとめて小学生用に本にすること。
編集者
ナゾロジー 編集部