X+X=2Xではありませんでした。
複雑な結び目同士を繋げると「予想よりも少ない手数」でほどけてしまう──そんな奇妙な現象がアメリカのネブラスカ大学リンカーン校(University of Nebraska–Lincoln)の研究によって数学的に初めて証明されました。
従来、結び目Aをほどくのに3回、結び目Bをほどくのに3回必要ならば、2つをつなげた場合には当然合計6回が必要と考えられていました。
しかし今回の研究では、そのような結び目が実際には5回以下でほどける場合があることが明らかになったのです。
約90年近く数学界で信じられてきた常識が覆ったことで、結び目理論の研究には新たな道が開かれました。
しかし一体なぜ、複雑な結び目をつなげるとほどきやすくなるのでしょうか?
研究内容の詳細は2025年6月30日に『arXiv』にて発表されました。
目次
- 結び目理論の常識は実は誰も確かめていなかった
- 2つの絡まりは『足し算より少ない手数』でほどけた:トーラス結び目が明かした意外な事実
- なぜ結び目は『計算通り』にほどけないのか?数学が示す新たな視点
結び目理論の常識は実は誰も確かめていなかった

イヤホンのコードが絡まって困った経験は、誰にでもあるでしょうか?
私たちの日常には、靴ひもやコード類など、絡まってしまうと本当に厄介なものがたくさんあります。
実は、このような「絡まり」を数学的に研究している分野があります。
それが「結び目理論」です。
数学の世界では、絡まりを「結び目」と呼びます。
その絡まり具合を調べる方法の一つに、「ほどき数)」という考え方があります。
これは、「絡まった紐を完全にほどくためには、最低でも何回、紐を上下入れ替える必要があるか?」という数字です。
ほどき数が大きいほど、絡まり方が複雑だと言えるわけです。
ただし、このほどき数をきちんと計算するのは実はとても難しく、いまだに完全に分かっていない結び目がたくさんあります。
絡まりの研究は一見単純そうなのですが、実は非常に奥が深く難しい問題なのです。
そんな結び目の世界で数学者が注目しているのが、「連結和」という考え方です。
これは、2つの別々の結び目を紐でつなげて、1つの大きな結び目を作る操作を指します。
イメージとしては、2つの結び目を「電車のように連結させて」、一つの長い絡まりにしてしまうという感じです。
これまで数学者たちは、「2つの結び目をつなげると、それぞれの絡まり具合がそのまま合わさって、より複雑になるはずだ」と直感的に考えてきました。
直感的にもイヤホンコードのこんがらがった同じ塊が2つあれば、複雑さも2倍で解きほぐす労力も2倍必要になると思うでしょう。
しかし問題は、「常にピッタリと合計と同じになるのか?」ということでした。
たとえばほどき数が10のこんがらがりと20のこんがらがりが2つあった場合、それらを連結した大きなこんがらがりを解くほどき数は10+20でピッタリ30になるのでしょうか?
実は、この問題は数学的には厳密に確かめられておらず「きっと同じになるだろう」と数学者たちが暗黙の仮説として信じ続けてきただけだったのです。
そこで今回、ネブラスカ大学の数学者であるブリットナム氏とハーミラー氏は、この長年の疑問に真正面から挑むことにしました。
もし、結び目を二つ連結させた場合に、「それぞれのほどき数を足した数よりも少ない手数でほどけてしまう結び目」を発見できたら約90年信じられてきた数学の常識を覆す画期的な出来事となります。
研究者たちはそのような例を見つけられたのでしょうか?
2つの絡まりは『足し算より少ない手数』でほどけた:トーラス結び目が明かした意外な事実
このような結び目の反例が本当に存在するのでしょうか?
謎を解明するために、研究者たちはまず、具体的に調べられるような、分かりやすい結び目を用意して調査を進めました。
最初に研究者たちが注目したのは、「トーラス結び目」と呼ばれる特別な結び目です。
トーラス結び目というのは、ドーナツのような輪の形をしたもの(トーラス)の表面に、規則的なパターンで紐をぐるぐると巻きつけて作った結び目のことです。
このような結び目は、規則正しい形をしているため、数学者にとって非常に分析がしやすく、よく研究の対象にされています。
このトーラス結び目の中でも、特に有名で数学者によく知られている結び目があります。
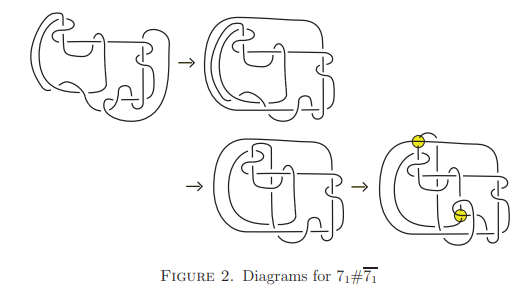
それは、「2回巻き」と「7回巻き」という規則的なパターンでトーラスの表面に巻かれた結び目(「(2,7)-トーラス結び目」と呼ばれるもの)で、数学者たちはこれを「7₁」という記号で表しています。
この「7₁」という結び目は、最低でも「3回」、紐の上下関係を入れ替えるような操作をしないと完全にほどけないことがすでに分かっています。
つまり、「7₁」はそれなりにほどくのが難しい結び目なのです。
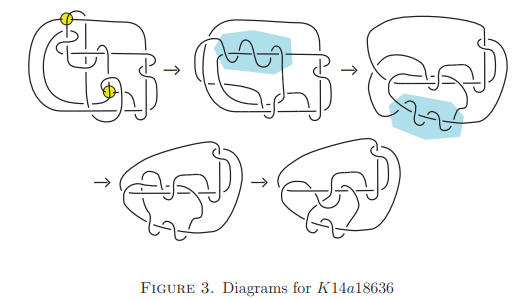
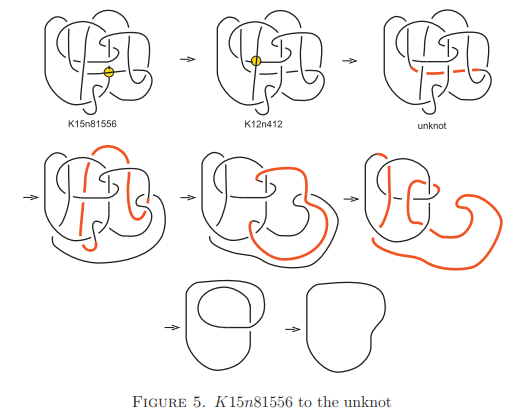
そこで研究チームは、この「7₁」の結び目を2つ用意して、一本の紐に順番に作り、「結び目の列車」のようにつなげて新しい結び目を作りました。
ここで直感的に考えると、1つの「7₁」をほどくためには3回の操作が必要なので、2つつなげた場合、3回+3回の合計で6回ほどかなければ完全に絡まりが解けないはずです。
しかし、これまで誰も厳密に確かめていなかったため、研究者たちは本当にそうなるかどうかを確かめるために詳しく調べてみることにしました。
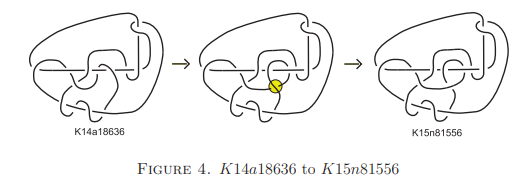
すると最初に複雑だった2つの「7₁」結び目をつなげた状態から、たった2回の操作で、やや簡単な絡まりに変化しました。
次にその絡まりをさらに1回の操作で、もっと簡単な絡まりに変えることができました。
そして最後に、その簡単になった結び目を2回の操作だけで完全にほどくことができたのです。
こうして最初の状態から完全に絡まりが解けるまでに必要だった操作回数は「2回+1回+2回」で、合計5回だけでした。
これには研究者たちも驚きを隠せませんでした。
なぜなら、当初は「3回+3回=6回」の操作が必要だと信じられてきたからです。
つまり、「2つの複雑な絡まりをつなげると、かえって予想より簡単にほどけてしまう」という現象が実際に証明された瞬間だったのです。
さらに研究チームは、このような現象が他にもないかを詳しく調べました。
すると、この現象は決して特別な一例だけに起きる珍しいものではなく、実際には数多くの結び目の組み合わせで同じようなことが起こり得ることを突き止めました。
つまり、「2つの絡まりをつなげると予想よりほどきやすくなる」という現象は広く存在し、決して特殊な例外ではないことが示されたのです。
こうして数学者たちが約90年間信じ続けてきた常識が、ついに覆りました。
「結び目をほどくための操作回数(ほどき数)は、2つつなげた場合には単純に足し算される」という考えが間違いだったことがはっきりと分かりました。
しかし、ここで新たな大きな疑問が生まれます。
なぜ、2つの複雑な結び目を連結すると、予想より簡単にほどけてしまったのでしょうか?
この意外な現象が起こる背後には、いったいどのような仕組みや理由が隠されているのでしょうか?
なぜ結び目は『計算通り』にほどけないのか?数学が示す新たな視点

今回の研究によって、「複雑な結び目同士をつなげると、逆に簡単にほどけてしまう場合がある」ことが示されました。
この発見は数学の研究だけに留まらず、私たちの日常生活や社会に対しても興味深い示唆を与えます。
例えば、イヤホンコードや荷物の紐の絡まりを考える際にも、『複雑な絡まりは必ずしも見た目通りの難しさとは限らない』という直感を与えてくれます。
さらに、DNAの分子やタンパク質が体内でどのように絡まり合っているかという生物学的な問題や、通信やデータ管理における暗号理論、さらにはコンピューターが難問を解決するための機械学習の手法に至るまで、幅広い分野への応用も考えられます。
つまり、この研究は、私たちが結び目という現象を新たな視点から捉え直すことで、意外な発見や革新的な方法が生まれる可能性を示唆しているのです。
また、この発見が数学者に対して特に大きな影響を与えたのは、結び目理論の根本にある「複雑さ」の概念を見直す必要性が出てきた点です。
【コラム】なぜ複雑+複雑は2倍の複雑にならないのか?
「なぜ複雑+複雑は2倍の複雑にならないのか?」残念ながら、研究を行った数学者たちも、その背後にある明確なメカニズムをまだ完全には解明できていません。しかし、彼らはこの驚くべき現象について、一つの重要なヒントを与えています。それは、「私たちが『結び目をほどく』という操作を理解しているつもりでも、実は見えていない部分がまだあるかもしれない」ということです。結び目をほどくための最短の手順を探すことは、実は非常に難しい問題です。数学者たちは、「絡まりをほどく最も良い方法はこれだ」と決めつけてしまいがちですが、実際には思いもよらないルートが隠されているかもしれないのです。今回の研究で見つかった反例は、まさにそのことを示しています。二つの結び目が連結された時、絡まり方が変化し、「それぞれを単独でほどく時とはまったく異なる、新たなほどき方」が生まれる可能性があるのです。これは例えば、2つの複雑なパズルを組み合わせた時に、予想もしていなかった解き方が浮かび上がるようなものです。それぞれ単独では難しい問題だったのに、組み合わさった瞬間、意外なほど簡単に解けるようになる、そんな逆説的な現象が起こっているのかもしれません。
これまで数学者は、結び目の複雑さを理解するために、「複雑な結び目を細かく基本的な結び目(素結び目)に分解して、それぞれの結び目の性質を足し合わせれば良い」と考えてきました。
しかし、今回の結果は、「複雑な絡まり同士の間に相互作用が生まれることで、足し合わせた以上の効果や予想外の簡単さが現れることがある」ということを意味しています。
これは結び目をほどくための実際の手法やアルゴリズムを作る上でも、新しいアイデアを提供する可能性があります。
また、この研究を通じて、SnappyやSageといったコンピューターを使った計算手法が結び目理論の難問を解く際に非常に強力であることも示されました。
つまり、この成果は結び目を研究する数学者に、実験的かつ計算的な手法の有効性を改めて示したという点でも重要です。
数学の世界では、一見当たり前と思われてきた法則が覆ることで新たな地平が開けることがしばしばあります。今回の成果もまさにその一例であり、結び目という身近で不思議な対象の奥深さを改めて示す出来事となりました。
元論文
Unknotting number is not additive under connected sum
https://doi.org/10.48550/arXiv.2506.24088
ライター
川勝康弘: ナゾロジー副編集長。 大学で研究生活を送ること10年と少し。 小説家としての活動履歴あり。 専門は生物学ですが、量子力学・社会学・医学・薬学なども担当します。 日々の記事作成は可能な限り、一次資料たる論文を元にするよう心がけています。 夢は最新科学をまとめて小学生用に本にすること。
編集者
ナゾロジー 編集部


